AI-Assisted Trading - Introduction (Part 1)

TLDR

In this post, I will cover concepts in reinforcement learning (RL), specifically Q-Learning, applied to the context of maximizing returns in a simulated stock market environment.

Enjoy!🙂

Q-Learning

As briefly described above, Q-Learning is an RL technique that learns the optimal strategy (called a policy in RL) from three distinct elements: the action space, the state space, and a reward function. Interestingly, the “Q” in Q-Learning comes from the act of focusing on the quality of each action, and choosing the best action.

In its simplest form, the algorithm has a function, $Q$, that calculates the quality of any state-action combination as follows: $$Q:\mathcal{S}\times \mathcal{A}\to \mathbb{R}$$

Actions

The action space, denoted $\mathcal{A}$, refers to the total number of possible actions a learner can take.¹ The cardinality (size) of $\mathcal{A}$ is determined by the number of actions to consider. In the context of a simulated market, we have 3 possible states: buy, sell, and exit market (going from a long/short position to holding 0 shares). When given some data, the Q-Learner will output a discrete value representing hold, buy, and sell: $$\mathcal{A}=\{0,1,2\}$$

States

The state space, denoted $\mathcal{S}$, refers to all possible states of the learning environment at any given point in time. Determining the cardinality of the state space is tricky, as this number largely depends on our input features. Say, for example, we have 5 input features.

These input features must go through some function, $f(x)$, that turns the continuous data into a singular integer representing unique values for all of our features. The process of converting raw continuous data into a singular integer, regardless of the number of input features, is called discretization.

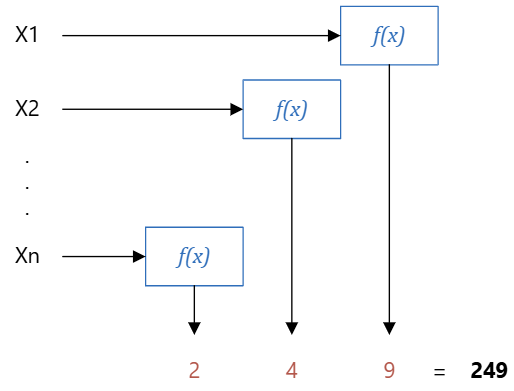
The function $f(x)$ should also slice the input vector into a number of bins. Each bin is then mapped to an integer. In the image above, feature $X_1$ is put into bin 9, $X_2$ into bin 4, and $X_n$ into bin 2. These integers are then spliced together to create one integer, $249$, that represents this combination of inputs.

Reward Function

Perhaps the most important pillar of a Q-Learner is the reward function, $R$. Of all the pillars, this should be most intuitive, especially for animal trainers. In this context, how do we reward our pets for making favorable decisions when training them to sit, or better yet, do a trick? Do we give them treats immediately after each success, or only once at the very end if they do everything right?

This decision will impact the time it will take for the learner to learn. Lots of questions need to be answered, mainly how do we reward our learner for making good trades, or penalize the learner for making subpar trades? What factors should be considered when making this decision? Do we base it on daily returns, or cumulative return for a prospective trade?

Q-Learners will converge to the optimal policy much faster when immediate reward is used.² In the context of pet training, immediately rewarding the animal after each success will help the animal to associate each action with positive reinforcement.

Conclusion

In this post, we’ve gone through an introduction to Q-Learning—the three pillars, what they mean, and how we can apply this in a simulated market. Simply put, a Q-Learner uses the current state and tries out different actions to see what happens.

Based on the reward of an action, it learns which actions are the best to take in similar situations in the future. We also covered discretization, or the process of representing continuous data as discrete integers, and the importance of this in determining states.

PART 2 »

References